Skaičių rodymas plokštumoje (apibrėžimas)

2024 Autorius: Leah Sherlock | [email protected]. Paskutinį kartą keistas: 2023-12-17 05:43

Gebėjimas teisingai atvaizduoti skirtingas formas lapo, drobės ir bet kurio kito paviršiaus plokštumoje yra gana svarbus įgūdis. Ir visų pirma tai svarbu ir meno žmonėms: tapytojams, skulptoriams, grafikams, dizaineriams (interjero erdvių ir architektūrinės aplinkos), ir mokslo žmonėms: matematikams, fizikai, dizaineriams, išradėjams.

Bet žmogui, kuris yra toli nuo šių sferų, taip pat svarbu išmokti teisingai suvokti ir rodyti jį supantį pasaulį. Tai padeda daug giliau suprasti visą jo universalumą. Jei neturite pakankamai supratimo, kaip tai padaryti teisingai, greičiausiai jums nepavyks sukurti jokio išradimo projekto, paveikslėlio ar brėžinio. Tai yra, šis įgūdis svarbus tiek sprendžiant paprastas, kasdienes užduotis, tiek tiems, kurie turi visuotinę, visuotinę reikšmę.

Šiek tiek istorijos

Nuo senų laikų žmonės stengėsi pavaizduoti tai, ką mato aplinkui: kitus žmones, kažkokius primityvius tų laikų pastatus, nuostabiai gražų augalų ir gyvūnų pasaulį, didingus kalnus ir tiesiog daiktus, namų apyvokos daiktus. Tai yra pasaulis su visa jo įvairove ir didybe.

Bet tada jie dar neįsivaizdavo, kaip tai galima padaryti tiksliai ir kompetentingai, kad įvairių trimačių objektų atvaizdavimas plokštumoje būtų tikrai tikroviškas, gyvas. Asmuo neturėjo atitinkamų žinių, be to, nebuvo ir ypatingų įgūdžių, išskyrus galbūt pačius elementariausius.

Ankstesniuose š altiniuose teigiama, kad pirmąjį paveikslą pasaulyje sudarė tik viena linija, einanti palei žmogaus šešėlį, kurį ant sienos meta saulė. Tai yra, pati gamta pasiūlė, kuria kryptimi verta judėti ieškant tinkamo šios problemos sprendimo.

Ir šis klausimas tuometinį žmogų jaudino ir dėl šios priežasties: jis ne tik norėjo grožėtis tūriniu gyvu siluetu, originaliu, galima sakyti, bet siekė užfiksuoti erdvinį objektą plokštumoje. Ir jis tai padarė, kad tokiu būdu galėtų papuošti savo namus ar jam šventą vietą, arba pasiimti su savimi ryšulį su paveikslu ir perkelti jį į bet kokį atstumą.

Rašto geometrija

Ir ką sakytumėte, bet bėgo metai, bėgo šimtmečiai ir kažkaip civilizacijai vystantis, žmonės palaipsniui išmoko rodyti sudėtingas figūras dvimatėje erdvėje, tai yra plokštumoje. Tik dabar pavaizduotų objektų dydžių ir proporcijų tikslumas pradėjo atrodyti labai apytikslis.

Tačiau klausimas, kaip teisingai atvaizduoti figūrą plokštumoje ir kiek jos atitinka originalių objektų tūrį, kartą tapo labai aktualus. Tam tikru būdu vadinamas naujas mokslasgeometrija. Tiksliau, jo atkarpa yra aprašomoji geometrija.

Čia ji tik tyrinėja formas ir plokštumas, linijas ir taškus, taip pat jų santykį vienas kito atžvilgiu – tiek trimatėje, tiek dvimatėje erdvėje.

Konversijos metodai

Svarbi vizualiųjų menų savybė yra figūrų rodymas vaizdo plokštumoje. Juk iš tikrųjų tai yra trimačių erdvinių objektų fiksavimas dvimatėje erdvėje. Būtent: kompleksas turi būti paverstas paprastu, tai yra, objektas, turintis ilgį, plotį, aukštį, turi būti perkeltas į plokštumą.

Ir aprašomoji geometrija daro tokius „perėjimus“dėl kai kurių metodų. Iš viso jų yra apie šešis. Štai trys pagrindiniai ir populiariausi visame pasaulyje:

• perspektyva (kai pavaizduotas objektas pašalinamas erdvėje);
• stačiakampė projekcija (lygiagreti projekcija, kai spinduliai statmeni plokštumai);
• įstriža projekcija (lygiagreti projekcija, kai spinduliai pakreipti plokštumos atžvilgiu).

Pavaizduotas objektas gana aiškiai matomas aksonometrinėje projekcijoje (įskaitant stačiakampę ir įstrižą). Tačiau aiškiausiai ir tikroviškiausiai jis projektuojamas, kai parodomas perspektyvoje. Ir būtent aukščiau pateikti metodai iš esmės išsprendžia klausimą, kaip pateikti figūras plokštumoje.

Perspektyva

Perspektyva užima garbingiausią vietą tarp kitų įvaizdžio metodų. Nes žmogaus akiskaip fotoaparato objektyvas, jis panašiai mato supančią erdvę. Daiktai, esantys toliau nuo stebėtojo, atrodo mažesnio dydžio, o kartais ir daug mažesni, nei tada, kai jie yra arti.

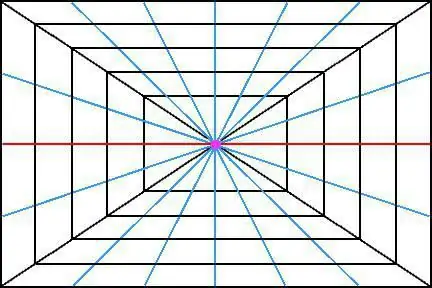
Pavyzdžiui, paimkite kubo vaizdą erdvėje. Jei iš tikrųjų visos jo briaunos yra lygiagrečios viena kitai, tai pažvelgus į šį objektą tolumoje gali atrodyti, kad briaunos susilieja (arba turėtų susilieti) viename taške. Ir, kas įdomiausia, jie turėtų ne tik susilieti viename taške, bet turėti vieną susikirtimo tašką.

Renesanso meistrų Albrechto Dürerio, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti dėka šiuolaikinė tapyba žino, kas yra tiesioginė linijinė perspektyva, kaip nustatyti horizonto aukštį ir nykstamus taškus.

Ir pasaulinio garso genijus Leonardo da Vinci pirmą kartą įrodinėjo oro perspektyvos koncepciją. Tai apima objekto spalvos, tono pasikeitimą, jo kontrasto charakteristikų pokyčius (mažėja objektui tolstant).

Ortografinė projekcija

Stačiakampė vadinama lygiagrečia projekcija, kuri nukreipta į tiesę, statmeną plokštumai. Jo taikymo procese objekto kontūrų matmenys išlieka nepakitę. Tai reiškia, kad objektas rodomas be iškraipymų.

Projektuojamas trimatis objektas tarsi išskaidomas į tris vaizdus: iš šono, iš priekio ir iš viršaus. Ir žiūrėdami į visa tai tuo pačiu metu, galite pridėtiatvaizdas, kaip objektas atrodo pagal tūrį. Tuo pačiu metu figūros matmenys išlieka nepakitę tiek trimačiame, tiek dvimačiame vaizde.

Įstriža projekcija

Ši projekcija suskirstyta į dar kelis porūšius, būtent:

• izometrinis vaizdas;
• dimetrinė projekcija;
• trimetrinė projekcija.

Izometrinė turi iškraipymo koeficientus visose 3 ašyse (ilgio, pločio, aukščio). Tai reiškia, kad kampai tarp poromis paimtų ašių yra lygūs 120 laipsnių. Dimetrinėje iškraipymai išilgai 2 ašių yra vienodi, o trečiosios skiriasi. O trimetinėje projekcijoje visi iškraipymo koeficientai (ty išilgai visų 3 ašių) yra skirtingi.

Sukimosi formos

Kai stačiakampis trikampis sukasi išilgai vienos iš dviejų kojų ašies, trečioji jo kraštinė (hipotenuzė) apibūdins naują figūrą, vadinamą kūgiu. Ir jei pasukate stačiakampį (kvadratą) išilgai vienos jo kraštinės, gausite cilindrą. Kai puslankis sukasi, išeis rutulys.

Iš to seka, kad sukant plokštumą išilgai kokios nors ašies gauname vadinamąsias sukimosi figūras.

Šios figūros turi sukimosi ašį. Kaip jie atrodo plokštumoje, priklauso nuo jų padėties akių lygio atžvilgiu. Pavyzdžiui, viršutinė ir apatinė cilindro pusės iš esmės yra apskritimai. Ir jei pažvelgsite į juos plokštumoje, jie atrodo kaip elipsės.

Tačiau užduotis tampa dar sunkesnė, jei rodomaerdvines figūras plokštumoje, jos turi pasvirusią ašį. Šiuo atveju svarbu, kad sukimosi kūnų kontūrai būtų vienodu atstumu nuo pastarosios ašies.

Šiek tiek apie chiaroscuro

Chiaroscuro vaidina svarbų vaidmenį rodant figūras plokštumoje. Mat vaizduojamo objekto tūris sukuriamas ne tik dėl linijų, bet ir dėl teisingo šviesos bei šešėlių pasiskirstymo jo šonuose. Ir tada jis atrodo gana didelis dvimačio paviršiaus plokštumoje.

Taigi, figūrų atvaizdavimas plokštumoje, jų dydžių nustatymas, teisingos šviesumo ir tamsių dėmių perdangos ypatybės yra visiškai įmanomas aukščiau aprašytų metodų dėka. Ir, svarbiausia, tai tikrai praktikoje patikrinti metodai, kuriuos taiko pirmaujantys mūsų laikų ekspertai.